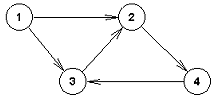
Slika 4
U usmerenom grafu razlikuju se ulazni stepen (broj grana čiji
kraj je čvor v) i izlazni stepen (broj grana za koje je čvor
v
početak).

Slika 4
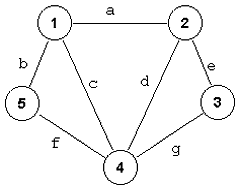
Na slici 4, stepen čvorova je:
| čvor | stepen | ulazni stepen | izlazni stepen |
|---|---|---|---|
| 1 | 2 | 0 | 2 |
| 2 | 3 | 2 | 1 |
| 3 | 3 | 2 | 1 |
| 4 | 2 | 1 | 1 |
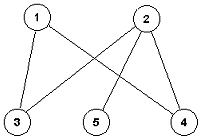
Čvor je u dostižan iz čvora v ako postoji put (usmeren/neusmeren)
od v do u. Po definiciji, čvor u je dostižan iz u.
v3, e1, v1, e2, v4, e5, v2, e6, v5, e3, v1, e2, v4 ( grana e2 se
pojavila dva puta)
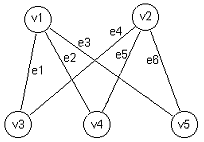
Slika 6
1, c, 3, f, 4, e, 2, d, 3 ( čvor 3 se pojavio dva puta)
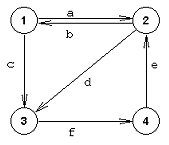
Slika 7
Ojlerov graf je povezan graf čiji čvorovi imaju paran stepen.
Graf na slici 10 sadrži Ojlerov ciklus predstavljen nizom čvorova
1, 2, 3, 5, 4, 1, 3, 4, 2, 5, 1.
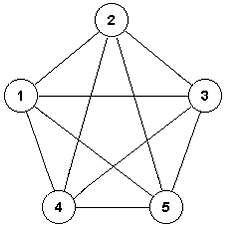
Slika 10
Graf H sa slike 12 je podgraf grafa G prikazanog na slici 11.
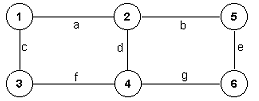
Slika 11
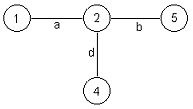
Slika 12
Graf G=(V,E) ima indukovani podgraf H=(U,F) ako H je podgraf grafa G tako da U je podskup od V i skup grana F sadrži sve grane skupa E tako da oba čvora grane su iz skupa čvorova U. Graf sa slike 14a ima kao indukovani podgraf graf sa slike 14b.
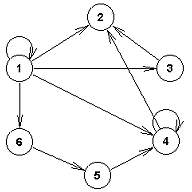
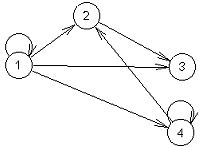
Problem topološkog sortiranja je problem formiranja rasporeda čvorova u grafu
G tako da ako se svi čvorovi grafa numerišu brojevima
od 1 do n=|V|, onda ako čvor v
je numerisan sa k svi čvorovi do kojih postoji
usmeren put iz v imaju numeraciju veću od k.
U glavi 6.4 knjige je prikazan algoritam za topološko sortiranje acikličkog usmerenog graga G.
Algoritam TOPSORT(G)
ulaz: G
izlaz: v.Num (numeracija cvora v u toploskom redosledu)
{
pomocu DFS obilaska stabla naci ulazni stepen svakog cvora, tj. v.InDeg
Broj=0; /*tekuci redni broj*/
for(i=1; i<=n; i++) if (v[i].InDeg==0) staviti v[i] u listu;
while (lista nije prazna)
{
uzmi cvor v sa liste;
Broj++; v.Num=Broj;
for svaka grana (v,w)
{ w.InDeg--;
if (w.InDeg==0) stavi w u listu;
}
}
}
Algoitam toploškog sortiranja je složenosti O( |E| + |V| ), tj. linearne složenosti kod grafova.
#include <stdio.h>
#define MAX 10 /*maksimalan broj cvorova*/
void topSortPoseti(int x, int a[][MAX], int n, int m[], int lista[], int *k);
/*obilazak grafa sa n cvorova zadatog matricom a pocev od neposecenog cvora x;
pri obilasku u nizu markiranih cvorova m vrednost clana m[x] ce postati 1, kad se poseti cvor x.
Kada se za cvor x zavrsi poseta svih nemarkiranih susednih cvorova,
cvor x se dodaje u niz lista na poziciju *k */
void topsort(int a[][MAX], int n, int lista[]);
/*DFS obilazak grafa G sa na cvorova zadatog matricom povezanosti a;
formiranje topoloskog redosleda cvorova u nizu lista*/
void ucitaj_matricu(int a[][MAX], int n); //ucitavanje grana grafa sa stdin
void trampa(int a[], int i, int j); //trampa clana a[i], a[j]
main()
{int a[MAX][MAX];
int n; //broj cvorova grafa
int lista[MAX];
scanf("%d", &n);
ucitaj_matricu(a,n);
topsort(a, n, lista);
}
void topSortPoseti(int x, int a[][MAX], int n, int m[])
{
int y; //cvor koji je u grafu potencijalni sused cvora x
m[x]=1; //markira se cvor x kao posecen
//ako postoji susedni cvor y koji nije markiran(m[y]=0), rekurzivno se poziva topSortPoseti za y
for (y=0; y<n; y++)
if( m[y]==0 && a[x][y]==1) topSortPoseti(y, a, n, m, x, &k);
lista[*k]=x; //ubacuje se cvor u topoloski uredjenu listu na kraj
k++; //priprema za prihvat sledeceg clana liste
}
void topsort(int a[][MAX], int n, int lista[])
{
int x, m[MAX],k;
/*cvor grafa x,
niz markiranih (posecenih) cvorova m,
k je index clanova topoloski uredjene liste cvorova */
k=0;
for (x=0; x<n; x++) m[x]=0; //na pocetku su svi cvorovi neposeceni
for (x=0; x<n; x++)
if (m[x]==0) topSortPoseti(x, a, n, m, lista, &k); //ako x nije posecen, pokrenuti topSortPoseti iz x
//kako smo cvorove dodavali u f-ji topSortPoseti na kraj lista, a ne na pocetak niza lista, mora se niz lista obrnuti
for(x=0; x<n/2; x++) trampa(lista, x, n-x-a); //trampe se prvi i poslednji, drugi i pretposlednji,...
}
void ucitaj_matricu(int a[][MAX], int n)
{
int i, j;
for (i=0; i< n; i++)
for(j=0; j<n; j++) a[i][j]=0;
while (scanf("(%d,%d)", &i, &j) != EOF) a[i][j]=1;
}
void trampa(int a[], int i, j)
{
int pom=a[i]; a[i]=a[j]; a[j]=pom;
}
2. Zadat je aciklički usmeren graf G=(V,E). Konstruisati algoritam linearne složenosti koji utvrđuje da li u G postoji neki prost put koji sadrži sve čvorove grafa.
REŠENJE:
Put je prost, ako se svaki čvor pojavljuje u njemu samo jednom.
U ovom zadataku zahtev je da se konstruiše algoritam za pronalazak Hamiltonovog puta u grafu G.
Ideja je da se konstruiše topološki redosled čvorova grafa G, a potom se proveri da li postoji put tako što se proveri da li susedni čvorovi u topološkom redosledu jesu putno povezani. Ukoliko su povezani, onda Hamiltonov put čine topološki uređeni čvorovi.
U glavi 6.4 knjige je prikazan algoritam za topološko sortiranje acikličkog usmerenog graga G.
Algoritam toploškog sortiranja je složenosti O( |E| + |V| ), tj. linearne složenosti kod grafova.
3. Neka G=(V,E) je neusmeren povezan graf koji ima k čvorova i svi su neparnog stepena. Dokazati da broj k je paran.
Neka d(1), d(2), ..., d(k) su stepeni čvorova.
Kako su oni neparni brojevi, možemo ih predstaviti kao d(i)=2*xi
+1, gde xi
su celi brojevi
Otuda zbir stepena svih k čvorova DEG=d(1)
+ d(2) + ... +
d(k) = 2*(x1 + x2 + xk ) + k
(*)
LEMA: DEG je paran broj.
Dokaz leme: Neka broj grana grafa |E|=s. Tada DEG=2*s, jer svaka grana
sadrži tačno dva čvora i pri računanju zbira stepena svih
čvorova (DEG) svaka grana se broji tačno dva puta, te je DEG dva puta veći od
ukupnog broja grana.
Dakle, prema (*) i prema lemi važi:
DEG=DEG
2*(x1 + x2 + xk ) + k
= 2*s
k = 2*(s- (x1 + x2 + xk )
)
Odavde zaključujemo da k je paran broj.
4.Granama grafa G=( {1,2,3,4}, E) su pridružene težine
kao u tabeli:
| grana | težina |
|---|---|
| (1,2) | 2 |
| (1,3) | 8 |
| (2,3) | 3 |
| (2,4) | 4 |
| (3,4) | 7 |
| (4,1) | 5 |
Odrediti sve najkraće puteve (all shortest paths) između čvorova ovog grafa.
REŠENJE: Matrica Wi se formira prema algoritmu izloženom i knjizi u odeljku 6.7
Algoritam SviNajkraciPutevi (W)
{ for (m=0; m<|V|; m++)
for(x=0; x<|V|; x++)
for(y=0;y<|V|; y++)
if ( W[x,m] +W[m,y] <W[x,y]) W[x,y]= W[x,m] +W[m,y] ; /*nadjen je kraci put od x do y od predjasnje postavljene duzine*/
}
| W 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | 0 | 2 | 8 | beskonačno |
| 2 | beskonačno | 0 | 3 | 4 |
| 3 | beskonačno | beskonačno | 0 | 7 |
| 4 | 5 | beskonačno | beskonačno | 0 |
| W 1 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | 0 | 2 | 8 | beskonačno |
| 2 | beskonačno | 0 | 3 | 4 |
| 3 | beskonačno | beskonačno | 0 | 7 |
| 4 | 5 | 7 | 13 | 0 |
7=5+2 13=5+8
| W 2 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | 0 | 2 | 5 | 6 |
| 2 | beskonačno | 0 | 3 | 4 |
| 3 | beskonačno | beskonačno | 0 | 7 |
| 4 | 5 | 7 | 10 | 0 |
5=2+3 6=2+4 10=5+5
| W 3 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | 0 | 2 | 5 | 6 |
| 2 | beskonačno | 0 | 3 | 4 |
| 3 | beskonačno | beskonačno | 0 | 7 |
| 4 | 5 | 7 | 10 | 0 |
| W 4 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | 0 | 2 | 5 | 6 |
| 2 | 9 | 0 | 3 | 4 |
| 3 | 12 | 14 | 0 | 7 |
| 4 | 5 | 7 | 10 | 0 |
9=4+5 12=7+5 14=7+7
5. Zadat je težinski graf iz prethodnog zadatka sa nenegativnim težinama grana. Naći središte grafa.
REŠENJE:Središte grafa je čvor v takav da ima najamanju ekscentričnost.
Ekscentričnost čvora v je maksimum najkraćih rastojanja od svih
čvorova grafa G do čvora v, tj.
ecc(v) = max { W[ i, v] | za svaki čvor i
}
| W 4 = W | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | 0 | 2 | 5 | 6 |
| 2 | 9 | 0 | 3 | 4 |
| 3 | 12 | 14 | 0 | 7 |
| 4 | 5 | 7 | 10 | 0 |
6. Zadat je težinski graf G=(V,E) sa nenegativnim težinama grana. Za zadata dva čvora i,j skupa V pronaći put minimalne dužine (a ne samo težinu tog puta).
REŠENJE:
BSO, indeksiramo vrste i kolone od 1..n umesto od 0 do n-1.
Izmena algoritma Svi_Najkr_putevi (glava 6.7 knjige) , tako da se
formira matrica prethodnika P gde element P[i,j]
pamti
čvor koji je neposredni prethodnik čvora j
na najkraćem putu od čvora i.
Jasno je da:
1. P[i,j]=0 ako je i==j ili ako W[i,j]=beskonacno
2. P[i,j]=i ako i !=j i ako w[i,j] < beskonacno
Dakle, najpre se algortmom Svi_najkraci_putevi u tri for ciklusa ažurira polazna matrica težina W, tako da na kraju čuva samo najkraće težine (rastojanja) između dva čvora. Tokom ažuriranja matrice W, vrši se i formiranje matrice čvorova P, tako što:
Potom se od dobijene matrice P rekonstruiše najkraći put u proceduri putanja.
Algoritam Svi_najkraci_putevi (W)
Ulaz:W(matrica tezina)
Izlaz: W(matrica duzina najkracih puteva), P(matrica prethodecih cvorova na najkracim putevima)
{
for (k=1; k<=n; k++)
for (i=1; i<=n; i++)
for (j=1; j<=n; j++)
if ( W[i,j]>W[i,k]+W[k,j] )
{ P[i,j]=P[k,j];
W[i,j]=W[i,k] + W[k,j]
}
}
/*iz matrice P rekonstruisemo najkraci put izmedju dva zadata cvora i,j */
Algoritam PUTANJA(i,j)
{
if (i==j)
stampati (i); /*povratak*/
else
if (P[i,j]==0) stampati "(Nema puta izmedju i, j)";
else
{PUTANJA(i, P[i,j] );
stampati (j);
}
}
Na primer, neka rezultujuća matrica P (po grafu iz zadatka 30 i 31) izgleda:
| 0 | 1 | 2 | 2 |
| 4 | 0 | 2 | 2 |
| 4 | 4 | 0 | 3 |
| 4 | 1 | 2 | 0 |
Tad je:
prvi poziv npr. Putanja (1,4)
kako P[1,4] !=0, drugi poziv je Putanja (1,2), jer P[1,4]=2
kako P[1,2] !=0, drugi poziv je Putanja (1,1), jer P[1,2]=1
kako 1==1, stampa se 1
dalje, štampa se 2
dalje, štampa se 4
DAKLE, najkraći put izmedju čvorova 1 i 4 jeste dužine 6 (po zadatku 30),
a ima putanju (((1),2),4)
7. Zadat je težinski usmeren graf G=(V,E) sa nenegativnim težinama grana. Konstruisati algoritam za određivanje ciklusa minimalne težine u G.
REŠENJE:
Iskoristićemo rešenje prethodnog zadatka. Naime, ciklus je put koji počinje i završava se u istom čvoru. Algoritam za nalaženje svih najkraćih puteva iz prethodnog zadatka se može iskoristiti za nalaženje najkraćeg ciklusa, tj. puta od čvorova i do čvora j preko čvorova 1, 2,...,k (najkraći k-put), redom za k=1,2,...,|V|.
Jer, nakon izvršenja algoritma za nalaženje svih najkraćih puteva iz prethodnog zadatka, težina (dužina, cena, ...) najkraćeg ciklusa je jednaka vrednosti najmanjeg elementa na dijagonali matrice W, tj. W[k,k] za k=1,2,...,n, gde n=|V|.
Ako je potrebno naći ne samo težinu najkraćeg ciklusa, već i sam put, onda se kao u prethodnom zadataku formira matrica prethodnika P gde element P[i,j] čuva čvor koji je neposredni prethodnik čvora j na najkraćem putu od cvora i.
BSO, indeksiramo vrste i kolone od 1 do n i pretpostavimo da ako dva cvora nisu vezani granom, njihova duzina puta je neki INT_MAX
Algoritam Najkraci_ciklus (W)
Ulaz:W(matrica tezina)
Izlaz: W(matrica duzina najkracih puteva), P(matrica prethodecih cvorova na najkracim putevima),
min (duzina najkraceg ciklusa)
{
for (k=1; k<=n; k++)
for (i=1; i<=n; i++)
for (j=1; j<=n; j++)
if ( W[i,j]>W[i,k]+W[k,j] )
{ P[i,j]=P[k,j];
W[i,j]=W[i,k] + W[k,j]
}
min=W[1,1]; k=1;
for(i=1;i<=n;i++) if (W[i,i]<min) {min=W[i,i]; k=i;}
PUTANJA(k, P[k,k]);
}
/*iz matrice P rekonstruisemo najkraci put izmedju dva zadata cvora i,j */
Algoritam PUTANJA(i,j)
{
if (i==j)
stampati (i); /*povratak*/
else
if (P[i,j]==0) stampati "(Nema puta izmedju i, j)";
else
{PUTANJA(i, P[i,j] );
stampati (j);
}
}
8. Zadat je težinski usmeren graf G=(V,E) u kom neke grane imaju negativnu težinu. Konstruisati efikasan algoritam za utvrđivanje da li graf sadrži ciklus negativne težine u G (dovoljno je dati rezultat u obliku odgovora DA/NE).
REŠENJE:
Primenimo ponovo algoritam Svi_Najkr_putevi (glava 6.7 knjige), ali ga modifikujmo tako da algoritam vrati odgovor DA kada naidje na dijagonalni element matrice koji je negativan.
BSO, indeksiramo vrste i kolone od 0..n-1 umesto od 1 do n
Algoritam Negativan_ciklus (W) Ulaz:W(matrica tezina) Izlaz: DA/NE u slucaju da ima/nema negativnog ciklusa { for (k=0; k<n; k++) for (i=0; i<n; i++) for (j=0; j<n; j++) if ( W[i,j]>W[i,k]+W[k,j] ) W[i,j]=W[i,k] + W[k,j] for(i=0;i<n;i++) if (W[i,i]<0) return DA;
return NE;
}9. Zadat je težinski graf G=(V,E) čije grane mogu imati i negativne težine. Naći najkraća rastojanja od polaznog čvora grafa G do svih ostalih (bez smanjenja opštosti obeležimo taj čvor sa 1).
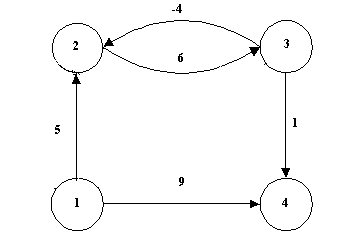
REŠENJE:
Koristimo Dijkstrin algoritam za nalaženje težina najkraćih puteva od zadatog čvora 1 do ostalih čvorova u grafu (glava 6.5 u knjizi) tako što ga modifikujemo da radi i nad težinski grafom G=(V,E) čije grane mogu imati i negativne težine.
Algoritam Dijkstra_negativni(G,W)
ulaz: G=(V,E) (tezinski graf sa negativnim tezinama), W(matrica tezina, indeksirana po i=1..|V| ) )
izlaz:D (niz gde d[i] je najkrace rastojanje od polaznog cvora 1 do cvora i, gde i=1..|V| )
T(niz gde t[i] je cvor koji je prethodnik cvora i na najkracem putu od cvora 1 )
{
for (i=2; i <= n; i++)
{
d[i]=w[1,i];
if (w[1,i] != beskonacno) t[i]=1;
else t[i]=0;
}
for (k=1; k<=n-1; k++)
for svaka grana (u,v)
if (d[u] +w[u,v] < d[v])
{
d[v]=d[u]+w[u,v];
t[v]=u;
}
for svaka grana (u,v)
if (d[u] +w[u,v] < d[v]) return false;
return true;
}
Na vremensku složenost algoritma utiču dva for ciklusa gde se za k=1..n-1
ažurira za svaka granu nizove D,T (ako je potrebno), te je onda složenost
O(
n |E| ).
10. Dat je usmereni graf G=(V,E) sa skupom čvorova V={1,2,3,4,5,6,7,8,9} i skupom grana E sa težinama kao na slici. Odrediti težine najkraćih puteva od čvora 1 do ostalih čvorova u grafu.
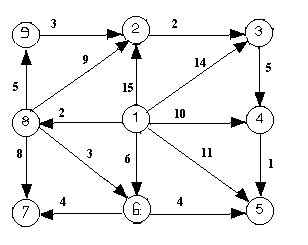
REŠENJE Koristimo Dijkstrin algoritam za nalaženje težina najkraćih puteva od zadatog čvora 1 do ostalih čvorova u grafu (glava 6.5 u knjizi).
Algoritam Najkr_putevi (G,v)
ulaz: G=(V,E) (tezinski usmeren graf), v (polazni cvor)
izlaz: za svaki cvor w je sa w.SP oznacena tezina najkraceg puta od v do w
(* uz pretpostavku da su sve tezine grana grafa nenegativne *)
begin
for svi cvorovi w do
w.oznaka=false;
w.SP=*; (* za sada tezina je beskonacna *)
v.SP=0;
while postoji neoznacen cvor do
neka w je neoznacen cvor sa najmanjom vrednoscu w.SP
w.oznaka=true;
for sve grane (w,z) takve da z je neoznacen do
if w.SP + tezina(w,z) < z.SP then z.SP=w.SP + tezina(w,z);
end
Prikaz postupka i rešenje je naveden u tabeli .
Najpre se popuni 1. red tabele tako da se unesu vrednosti
težina grana sa slike grafa.
Potom se izabere najmanja težina te vrste. Konkretno to je
ovde vrednost 2 čvora 8.
Potom se označi čvor 8 i formira 2. red tabele u kom se menjaju
težine onih puteva koje bivaju kraće ako se u njih uključi čvor 8.
I tako redom sve dok postoji neoznačen čvor.
| označeni | čvor w
(najmanje SP) |
2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | - | 15 | 14 | 10 | 11 | 6 | * | 2 | * |
| 1,8 | 8 | 11 | 14 | 10 | 11 | 5 | 10 | 2 | 7 |
| 1,6,8 | 6 | 11 | 14 | 10 | 9 | 5 | 9 | 2 | 7 |
| 1,6,8,9 | 9 | 10 | 14 | 10 | 9 | 5 | 9 | 2 | 7 |
| 1,5,6,8,9 | 5 | 10 | 14 | 10 | 9 | 5 | 9 | 2 | 7 |
| 1,,5,6,7,8,9 | 7 | 10 | 14 | 10 | 9 | 5 | 9 | 2 | 7 |
|---|---|---|---|---|---|---|---|---|---|
| 1,2,5,6,7,8,9 | 2 | 10 | 12 | 10 | 9 | 5 | 9 | 2 | 7 |
| 1,2,4,5,6,7,8,9 | 4 | 10 | 12 | 10 | 9 | 5 | 9 | 2 | 7 |
| 1,2,3,4,5,6,7,8,9 | 3 | 10 | 12 | 10 | 9 | 5 | 9 | 2 | 7 |
11. Neka e je grana maksimalne težine u nekom ciklusu grafa G=(V,E). Dokazati da postoji MCST grafa G'=(V, E\{e}) koje je istovremeno i MCST grafa G.
REŠENJE:
PODSEĆANJE:
Prema glavi 6.6 knjige Algoritmika MCST (minimum-cost spanning tree) je minimalno povezujuće stablo, tj. povezujuće stablo čija suma težina (cena) grana je minimalna.
U knjizi je prikazan algoritam za konstrukciju MCST koji nalikuje Dijkstra algoritmu za nalaženje najkraćih puteva od zadatog čvora grafa. Složenost algoritma je O( (|E|+|V|) log |V|)
Neka T je MCST zadatog grafa G koje sadrži granu
e=(x,y) najveće težine u nekom ciklusu C. Ako se
ukloni grana e, onda iz stabla T nastaju stabla T1, T2, tako da je na
primer čvor x u T1, čvor y u T2.
Neka P je put od x do y koji nastaje kada se iz cilusa C ukloni grana e.
Na tom putu postoji grana e1 koja povezuje stabla T1 i T2, tj. grana čiji jedan
kraj mora biti u T1, a drugi kraj u T2. Težina grane e1 jednaka je težini grane
e (jer ako bi težina grane e1 bila manja od težine grane e, onda bi povezujuće
stablo T bez grane e koje sadrzi
granu e1 imalo manju cenu od stabla T).
Dakle, stablo (T\{e}) sa granom {e1} je MCST, ali ne sadrzi granu e.
12. Neka je G=(V,E) neusmeren težinski graf i neka T=(V,F) je podgraf koji se sastoji od svih grana na najkraćim putevima od čvora x iz V. Ako se težine grana G povećaju za jednu istu konstantu w, da li T ostaje i dalje stablo najkraćih puteva od x.
REŠENJE: Odgovor je NE.
Na primer, neka u grafu T sa korenom x i čvorovima x, y, z (trougao XYZ)
grana (x,y) ima
težinu 2
grana (x,z) ima težinu 5
grana (y,z) ima težinu 2
To znači da primenom Dijkstra algoritma nad G smo imali da u odnosu na granu (x,z) kraći put od x do z preko čvora y ima težinu 4=2+2
Neka je w=5. Dakle, sada u grafu T sa korenom x
grana (x,y) ima težinu 7
grana (x,z) ima težinu 10
grana (y,z) ima težinu 7
To znači da put od x do z preko čvora y ima težinu 14=7+7, ali od njega je kraća grana (x,z) sa težinom 10
13.
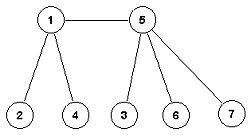
Dat je bipartitivni graf G čiji su
čvorovi a, b, c, d, e, f, g
odnosno 1, 2, 3, 4, 5, 6, 7 i
čiji skup grana je
{(a,1), (a,2), (a,5), (b,1), (b,2), (b,6), (c,1), (c,2), (c,3), (c,7), (d,1), (d,2), (e,1), (e,4), (f,5),
(g,6)}.
Odrediti optimalno bipartitivno uparivanje.
PODSEĆANJE:
Za zadati neusmeren graf G, uparivanje je skup
disjunktnih grana (grana bez zajedničkih čvorova).
Čvor koji ne pripada niti jednoj grani uparivanja zove se
neuparen čvor.
Savršeno uparivanje je uparivanje u kom su svi čvorovi upareni.
Optimalno uparivanje je uparivanje sa maksimalnim brojem grana. Ovaj
zadatak se bavi jednim tipom optimalnog uparivanja.
Teorema o alternirajućem putu:
Bipartitivno uparivanje S jeste optimalno
<= > u grafu G
ne postoje alternirajući putevi za njega.
Alternirajuci put X za dato uparivanje S jeste put od neuparenog
čvora v iz V do neuparenog
čvora u iz U, pri
čemu su grane puta X naizmenično u E\S, odnosno u S.
Tj. prva grana (v,x) puta X ne pripada S, jer v je neuparen, druga grana (x,y) pripada S i
tako dalje do grane (z,u) puta X koja ne pripada S.
Teorema o alternirajućem putu određuje korake algoritma za
pronalazak optimalnog bipartitivnog
uparivanja. Naime, ma koje uparivanje
koje nije optimalno ima alternirajući put, a alternirajući put proizvodi
povećano uparivanje. Dakle, na početku algoritma
pronadje se uparivanje S dodavanjem grana dokle god je to moguće. Potom se
pronadje alternirajući put za uparivanje S, a na osnovu njega se vrši
povećavanje uparivanj sve dok nedobijemo novo uparivanje S za koje nema
alternirajućih puteva. Dobijeno uparivanje je tada optimalno.
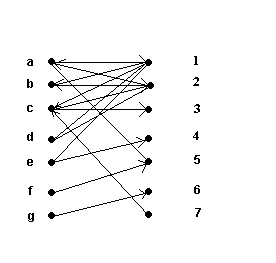 Dakle, neka je uparivanje M={(a,1), (b,2), (c,3), (e,4), (f,5), (g,6)}.
Dakle, neka je uparivanje M={(a,1), (b,2), (c,3), (e,4), (f,5), (g,6)}.
Na slici je prikazano da zbog pronalaska alternirajuceg puta u G, usmeravamo grane G tako da one koje su u M budu udesno, a one koje nisu orjentisane su ulevo. Neupareni su čvorovi 7, d i pokušavamo da nadjemo put od 7 do d. Ali takav put ne postoji, jer od 7 se može samo do čvora c, a od njega dalje samo do čvora 3, ali ne i čvora d. Dakle, M je optimalno uparivanje.
Može se do uparivanja M doći i ako se kao polazno uparivanje uspostavi uparivanje N={(a,5), (b,2), (c,3), (e,4), (g,6)}, jer bi se uočio alternirajući put f, 5, a.
14.
Dat je bipartitivni graf G čiji su
čvorovi a, b, c, d, e, f, odnosno 1, 2, 3, 4, 5, 6 i
čiji skup grana je
REŠENJE:
{(a,1), (b,1), (b,2), (b,3), (c,4), (d,3), (d,6), (e,4), (f,5), (f,6)}.
Odrediti optimalno bipartitivno uparivanje.
Za zadati neusmeren graf G, uparivanje je skup
disjunktnih grana (grana bez zajedničkih čvorova).
Čvor koji ne pripada niti jednoj grani uparivanja zove se
neuparen čvor.
Savršeno uparivanje je uparivanje u kom su svi čvorovi upareni.
Optimalno uparivanje je uparivanje sa maksimalnim brojem grana. Ovaj
zadatak se bavi jednim tipom optimalnog uparivanja.
Ako
G=(V,E,U) jeste bipartitivni graf u kome V, U su disjunktni skupovi čvorova, E
je skup grana koje povezuje neke čvorove iz V sa nekim čvorovima iz U.

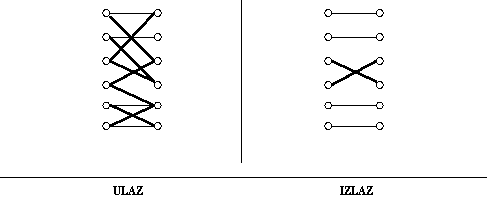
Neka je uparivanje S={ a-1, b-3, c-4,
d-6}.
Može se uočiti da postoji alternirajući put za ovo
uparivanje i to je put a-1-b-3-d-6-f. Kako postoji alternirajući put=>ovo uparivanje u G nije
optimalno.
Granu b-3 i dodamo nove grane b-2, f-6. Novo uparivanje S={
a-1, b-2, c-4, d-3, f-6}.
Novo uparivanje nema aternirajućih puteva (jer bi tačno jedan takav
bio e-4-c-5, ali on ne može da se realizuje u G)=> uparivanje
S jeste optimalno. (broj grana u uparivanju je pet i
jeste optimalno , jer postoji tačno po jedna grana za
čvor c, odnosno e i to do čvora 4)